Basics Of Mechanical Vibrations- Simple Harmonic Motion

Simple Harmonic Motion

Simple represents a straight line and harmonic motion represents periodic motion. In simple terms, simple harmonic motion is a straight-line periodic motion. Following are the characteristics of an object under simple harmonic motion.

Characteristics of Simple Harmonic Motion

The restoring force is always directed towards the mean equilibrium position. Hence the restoring force has a negative sign that indicates the direction of force is opposite to the displacement.
The acceleration of the particle is proportional to the displacement of an object from its mean position.
The direction of oscillation is opposite to the direction of displacement.

Mean equilibrium position or mean position: The position of an object where the net force acting on the object is zero.

Example-1 of Simple Harmonic Motion “Spring-Mass System”

Consider a classic example of a spring-mass system as shown in the figure below.

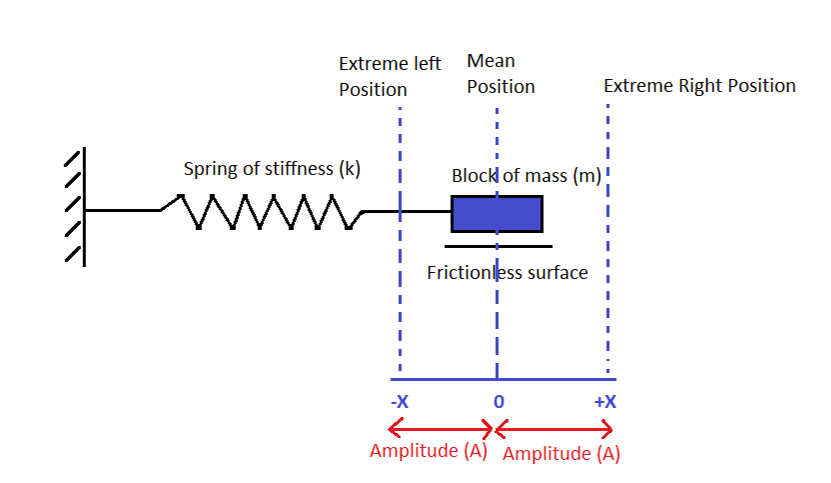
word image 2223 1 — ***Figure 1: Typical Spring Mass system under oscillation***

Assumptions:

The spring always is in an elastic state. (Such that Hook’s law is applicable)
Neglect the friction between the block and its contact surface with the floor.
Neglect the air resistance surrounding the block of mass (m).
Neglect the mass of spring.

Displace the block from its mean position i.e., push it towards positive X-direction as shown in the figure-1. Apply Newton’s second law of motion. (Object acted upon by a force, will accelerate in the direction of force)

$\sum F_{x}=m\, a_{x}$

$F_{s}=m \, a$

$-k\, x=m \, a$

$a=\frac{-k}{m}x$ ——-Eq-1

The equation-1 satisfies the characteristics of simple harmonic motion.

Spring force is the restoring force.
Acceleration is proportional to displacement.
The direction of acceleration is opposite to displacement.

Hence the motion of the block is in simple harmonic motion.

From equation-1,

$m\frac{\mathrm{d^{2} x} }{\mathrm{d} t^{2}}=-kx$

$\frac{\mathrm{d^{2} x} }{\mathrm{d} t^{2}}=\frac{-k}{m}x$

$\frac{\mathrm{d^{2} x} }{\mathrm{d} t^{2}}=-\omega^{2}x$ —Eq-2

Equation-2 is called governing differential equation of a simple harmonic motion. From equation-2, it can be seen that $(k/m) \, or \, \omega^{2}$ is a constant value. The choice of solution function for the above differential equation should be such that the second derivative of the function is the same as of original one.

$x(t)=A\, cos(\omega t+\phi)$ is right solution.—–Eq-3

Where,

A represents the amplitude of motion
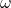$\omega$ represents the angular frequency.
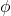$\phi$ represents phase constant.

Note:

A bouncing ball on the floor is not in Simple Harmonic Motion because the acceleration of the ball at the mean position i.e., at the time of contact with the floor is maximum. But whereas in Simple Harmonic Motion, acceleration is zero at the mean position.

Time Period of oscillation of spring mass system

The period of oscillation is defined as the time required to complete one full cycle.

From eq-2,

$\omega =\sqrt{\frac{k}{m}}$ ——————Eq-4

where $\omega \,$ represents the angular frequency.

From basic physics,

$\omega=2 \pi f=\frac{2 \pi}{T}$ —————-Eq-5

where f represents the simple frequency (cycles per second) and T represents the time period of oscillation.

By substituting Eq-4 in Eq-5,

Finally, the time period of oscillation of the spring-mass system is

$T=2\pi \sqrt{\frac{m}{k}}$

Example-2 of Simple Harmonic Motion “Simple Pendulum”

Consider a bob of mass (m) attached to a string of length (L) as shown in the following figure.

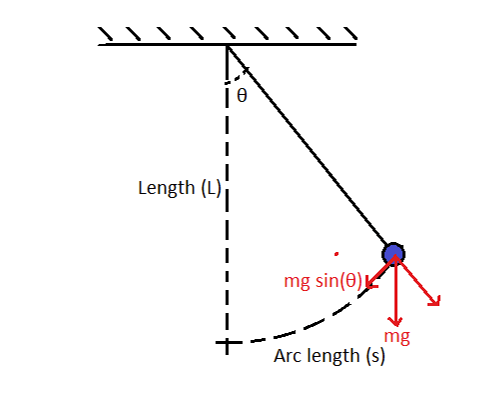
word image 2223 2 — ***Figure 2: Typical Simple Pendulum in oscillation***

By applying Newton’s second law of motion in the tangential direction, we get

$-mg \, sin \theta=ma$

$-g \, sin \theta= \frac{\mathrm{d}^{2}s }{\mathrm{d} t^2}$

Assumptions

Assuming the angular displacement 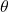$\theta \,$ is small,

$sin \theta \, \approx \theta$ where $\theta \,$ is in radians. The assumption holds good only if the $theta \leq 10^{o}$ .

From the figure-2,

$sin \theta = \frac{S}{L}$

$S=L \theta$

$L\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2}=-g\, \theta$

$\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2}=\frac{-g}{L}\, \theta$

$\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2}=-\omega^2\, \theta$ ——–Eq-6

Equation-6 is in a similar form of governing differential equation of simple harmonic motion i.e., Eq-2

Time Period of oscillation of a simple pendulum

From eq-6,

$\omega =\sqrt{\frac{g}{L}}$ —–Eq-7

where $\omega \,$ represents the angular frequency.

From basic physics,

$\omega=2 \pi f=\frac{2 \pi}{T}$

Finally, the time period of oscillation of a simple pendulum is

$T=2\pi \sqrt{\frac{L}{g}}$

Conclusions

The motion of a simple pendulum can be called simple harmonic motion only if the angular displacement ( 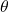$\theta$ ) is small.
The Time period of a simple pendulum is independent of the mass of the bob.
All the simple pendula of different mass and same string length at the same location have the same time period of oscillation.

Applications

By measuring the time period of the Simple pendulum at different locations, the location of valuable minerals and oil resources in the ground can be detected due to a change in the “g” value.

Example-3 of Simple Harmonic Motion “Torsional Pendulum”

Consider a disc attached to a massless shaft having a torsional stiffness (k) as shown in the following figure. The shaft is fixed at the top.

Assumptions

The shaft always is in an elastic state only. Such that Hook’s law is applicable.

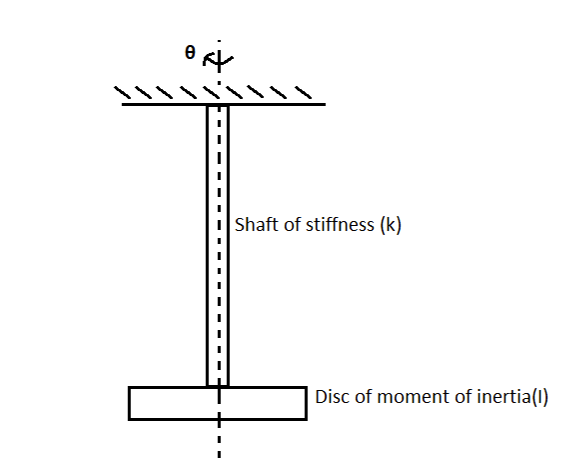
word image 2223 3 — ***Figure 3: Typical Torsional Pendulum***

Displace the disc angularly from its mean position and by applying newton’s second law of motion, we get

$\sum T=I\alpha$

$-k \theta = I \alpha$

$\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2}=\frac{-I}{k}\theta$ —Eq-8

The above equation is the same as a governing differential equation of simple harmonic motion. Hence the motion

Time Period of oscillation of a torsional pendulum

$T=2\pi \sqrt{\frac{I}{k}}$

Sign Up

Sign In

Forgot Password

The Mechanical Engineer Latest Articles

Table of Contents