Part-2 Magnification Factor And Transmissibility

Deformation Response Factor or Magnification Factor

Displacement of a Mass-Spring-Damper (MSD) system i.e., the vibratory response of a system subjected to harmonic load with respect to various frequency ratios ( $\frac{\omega} {\omega_{n}}$ ) is analysed in detail here.

Practical Application

Real-world machines like pumps, centrifugal fans, compressors…etc can be modelled as mass spring damper system, and their common defects like unbalance in impeller, misalignment, bent shaft…etc can be modelled as harmonic loads as shown in the figure below. Thus, a basic understanding of the response of an MSD system under harmonic load is highly essential for a maintenance engineer to predict the defect in the machine without dismantling it.

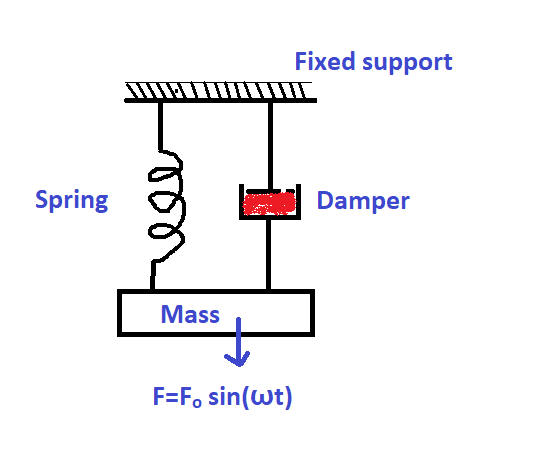
Figure 1 Mass Spring Damper system under harmonic load — ***Figure-1: Mass-Spring-Damper system under harmonic load***

As we discussed in the previous article, the response of an MSD system (as shown in the above figure) subjected to harmonic load is given as,

$u(t)= \frac{\frac{F_{o}} {k} sin(\omega t- \phi )}{\sqrt{[1-(\frac{\omega}{\omega {n}} )^{2})^2+(2\xi (\frac{\omega }{\omega_{n}}))^2]}}$ ——–Eq-1.

Since the transient response of an MSD system reduces exponentially with respect to time, the contribution of transient response to the total response (Total response = Transient + steady-state response) of a system is negligible. So, our focus is on the steady-state response of a system that exists as long as the system is running.

The term, $\frac{F_{o}}{k}$ represents the static deformation of the system due to the load $F_{o}$ . Since the static deformation of the system is independent of both natural as well as forcing frequency, it always exists irrespective of frequency. For the maximum amplitude, the eq-1 can be rewritten as,

$u(t)= \frac{F_{o}}{k} \times MF$

Where,

$MF = \frac{1}{\sqrt{[1-(\frac{\omega}{\omega {n}} )^{2})^2 +(2\xi (\frac{\omega }{\omega_{n}}))^2}}$ represents the magnification factor which magnifies the static deformation of the system depending on the frequency ratio $\frac{\omega}{\omega_{n}}$ .

Conclusion from the eq-1

1. At $\frac{\omega}{\omega_{n}} <<1 \,$ , the time period of force excitation is much higher than the natural frequency of the system. i.e., $T>>>T_{n}$ . Then, from eq-1

$u(t)= \frac{F_{o}}{k}$ —-Eq-3

It means at lower frequency ratios,

The vibratory response of a system is independent of damping.
The vibratory response of a system is controlled by the stiffness of the system. So, for the machinery having lower frequency ratios must be stiffer enough to reduce its vibration due to harmonic force (harmonic force is nothing but the induced load due to defects in the machinery like unbalance in the impeller, misalignment…. etc).
Though the harmonic force is a function of time but its frequency is very less as compared to the natural frequency of a system the system undergoes static deformation as per eq-3.

2. Similarly, at $\frac{\omega}{\omega_{n}} =1, \,$ time period of harmonic force is equal to the natural frequency of the system. i.e., $T=T_{n}$ . Then, from eq-1

$u(t)=\frac{F_{o}}{2k\xi } = \frac{F_{o}}{\omega _{n} c}$ —-eq-4

Since $\xi=\frac{c}{c_{c}}\, and \,c_{c}=2m \omega _{n}$

The vibratory response of a system is controlled by damping.
If the damping of a machine is zero then at the natural frequency the vibration amplitude of the machine is infinite which leads to catastrophic failure. Thanks for the steel which has the damping ratio in the range of 0.02 to 0.03.

3. Similarly, at $\frac{\omega}{\omega_{n}} >>1$ , the time period of force excitation is much lower than the natural frequency of the system. i.e., $T>>>T_{n}$ . Then, from eq-1

$u(t)=\frac{F_{o}}{\omega^{2} m}$ ——–eq-5

The vibratory response of a system is controlled by the mass of the system.
The vibratory response of a system is independent of damping.

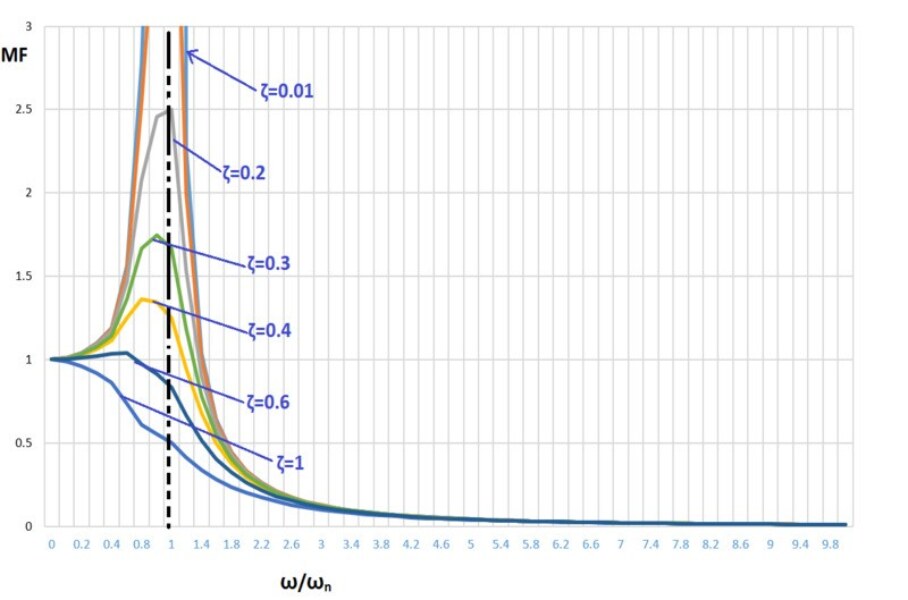
To analyse the eq-1 in detail, we plot the curve between MF and frequency ratio.

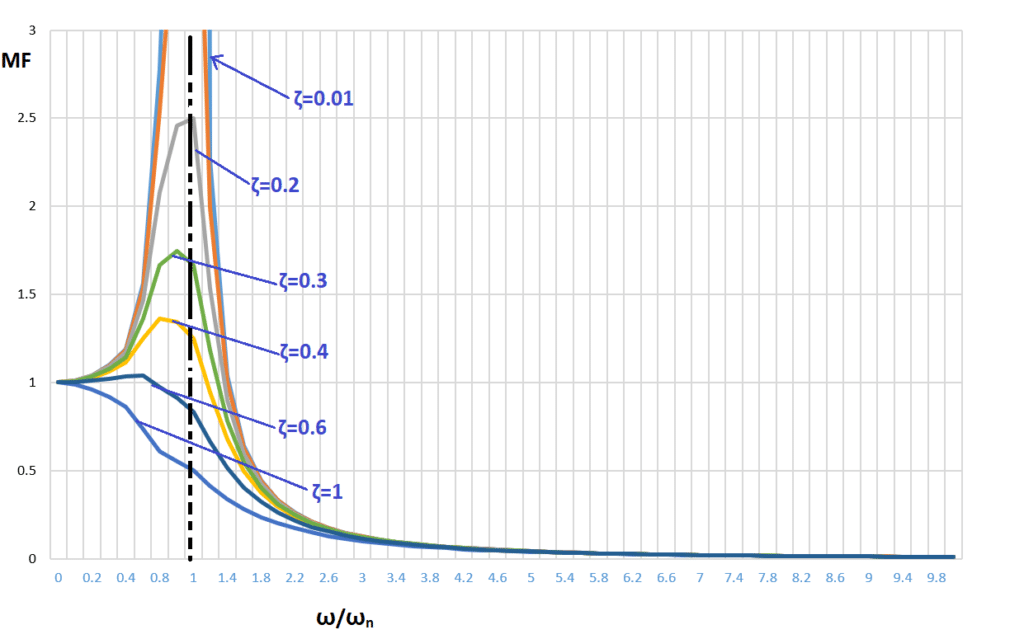
Figure 2 Magnification Factor vs Frequency ratio — ***Figure-2:Magnification Factor vs Frequency ratio***

Conclusion from the above graph

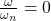$\frac{\omega}{\omega_{n}} =0$ , MF=1. It means at stationary conditions the system or machinery will have static deflection.(i.e. the response of a system is in the form of a sine wave with the maximum amplitude of $\frac{F_{o}}{k}$ .
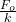As damping increases, the peak amplitude of vibration reduces. And the peak value shift towards the left for the displacement response of a system.
At very high-frequency ratios, i.e., heavy machines (have low natural frequency) running at very high speeds (have high excitation forcing frequency) have very less displacement and thus less vibrations.

Eq-1 represents the displacement of the system. The first derivative of displacement with respect to time yields the velocity response of the system. Similarly, the first derivative of velocity yields the acceleration response of the system.

$\dot{u}(t)=\frac{F_{o}}{k} \, \,MF \,\omega\,\,cos(\omega t-\phi)$ —-eq-6
$\ddot{u}(t)=\frac{F_{o}}{k} \, \,MF \,\omega ^2\,\,sin(\omega t-\phi)$ —eq-7

But the resonant frequencies of displacement, velocity and acceleration of the system are different. By doing $\frac{d(displacement\, or\, velocity\,or\, acceleration )}{d(\frac{\omega}{\omega_{n}})}=0$ we can get the frequency corresponding to the maximum amplitude which is nothing but resonant frequency. Following are the results.

Displacement resonant frequency = $\omega_{n}\sqrt{1-\xi^2}$ —eq-8
Velocity resonant frequency = $\omega_{n}$ —–eq-9
Acceleration resonant frequency= $\frac{\omega_{n}}{\sqrt{1-\xi^2}}$ ——eq-10

Note: While doing the bump test of a structure or machinery to find its natural frequency, always measure the peak amplitude of velocity instead of acceleration and displacement because the resonant frequency of velocity occurs directly at $\omega_{n}$ .

Transmissibility

Consider a centrifugal pump resting on the base (steel base frame). Let us assume that there is a defect (unbalance in impeller, misalignment, shaft bent…. etc) in the pump that led to the generation of harmonic load which results in vibration of the pump. It can be modelled as following the spring-mass damper system. The pump is modelled as a lumped mass and the base is modelled as a combination of spring having the stiffness K and damping factor C.

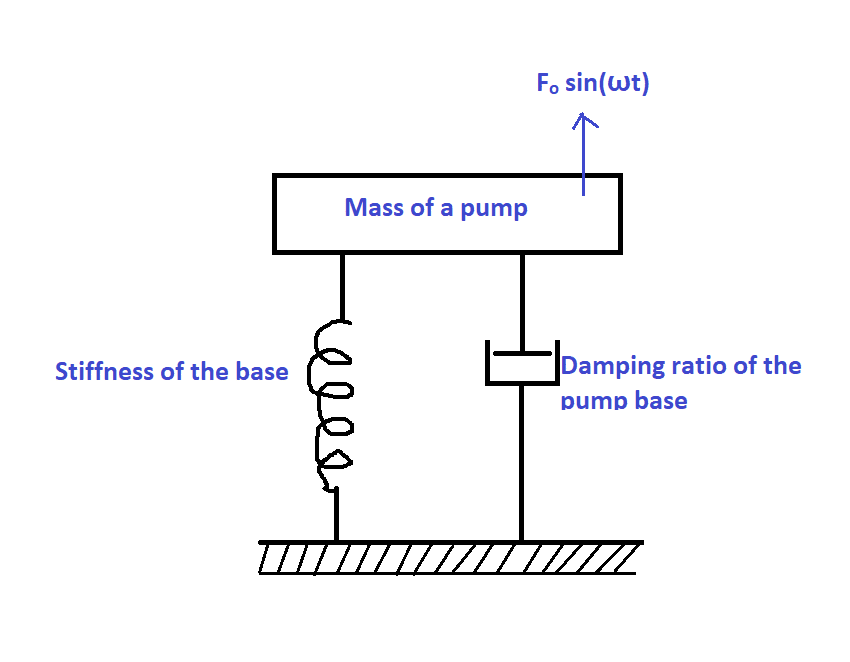
Figure 3 Spring mass damper model of a centrifugal pump and its base — ***Figure-3: Spring mass damper model of a centrifugal pump and its base***

We are interested in how much force is transmitted to the pump base due to the pump’s vibration. The transmissibility ratio (TR) is defined as the ratio of the maximum transmitted force to the applied force.

$TR=\frac{F_{t}}{F_{o}}= \sqrt{\frac{1+ (2\xi \frac{\omega}{\omega}_{n})^{2}}{[1-(\frac{\omega}{\omega {n}} )^{2})^2 +(2\xi (\frac{\omega }{\omega_{n}}))^2]}}$ ————eq-11

With the help of plot transmissibility ratio vs frequency ratio, equation-11 can be analysed in detail,

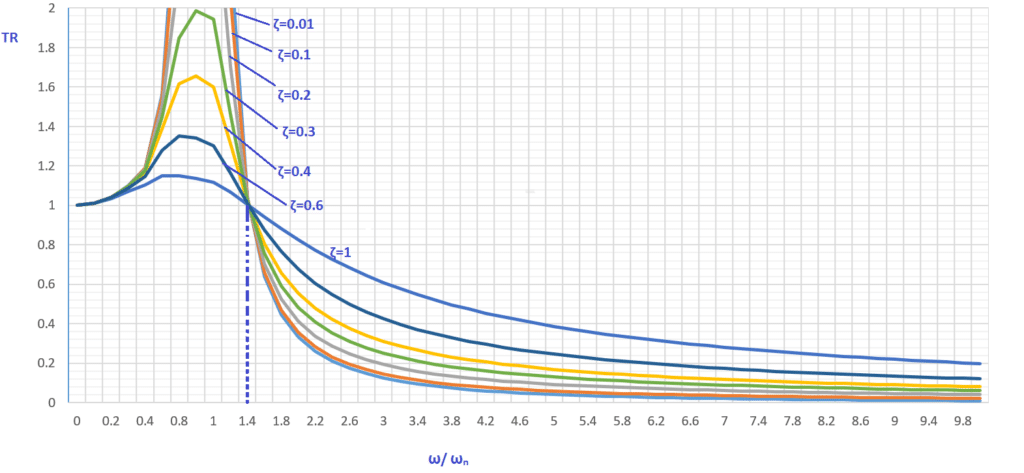
Figure 4 Transmissibility ratio vs frequency ratio — ***Figure -4: Transmissibility ratio vs frequency ratio***

Conclusion

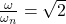At $\frac{\omega}{\omega_{n}}=0\,$ and $\frac{\omega}{\omega_{n}} =\sqrt{2} \,$ TR=1 irrespective of damping. It means whatever the force is generated by the pump it gets transmitted to the pump base.
At 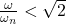$\frac{\omega}{\omega_{n}} <\sqrt{2} \,$ , an increase of base frame damping ratio reduces the transmissibility of the force to the pump’s base. So, for the machinery having high natural frequencies like small to mid-size centrifugal fans (having high natural frequency due to relatively less mass), vibration damper pads are installed between the machinery and its base to reduce the force transmission from the machine to its base.
At, 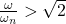$\frac{\omega} {\omega_{n}} >\sqrt{2} \,$ , the increase of base frame damping increases the transmissibility of force to the pump base. In general, heavy machinery like large reciprocating compressors (having low natural frequency since its mass is heavy) are installed directly to the base without any damping material between the machine and its base frame.

Sign Up

Sign In

Forgot Password

The Mechanical Engineer Latest Articles

Table of Contents

Deformation Response Factor or Magnification Factor

Practical Application

Conclusion from the eq-1

Conclusion from the above graph

Transmissibility

Conclusion

Related Posts

Basics of Mechanical Vibrations- Simple harmonic motion

Part-3 Vibration parameters: displacement, velocity, acceleration

Part-1 Basics of Mechanical Vibration