Table of Contents
Basics Elements of Mechanical Vibration
To utilize vibration analysis as a predictive maintenance tool to detect and diagnose the defects in a machine, the basic knowledge of vibration is essential. A complete understanding of the damped single degree of freedom system under harmonic load is necessary to master the vibration analysis. This article starts with the basics of mechanical vibration.
Any machine component will have the following three fundamental elements. They are
- Mass
- Stiffness
- Damping
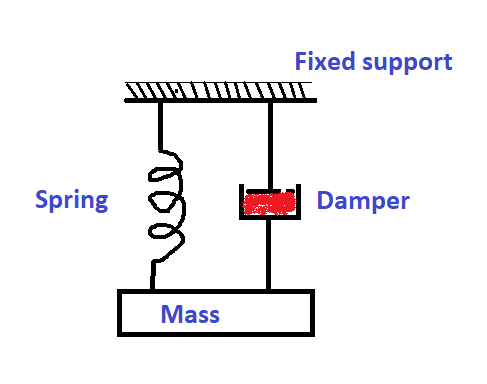
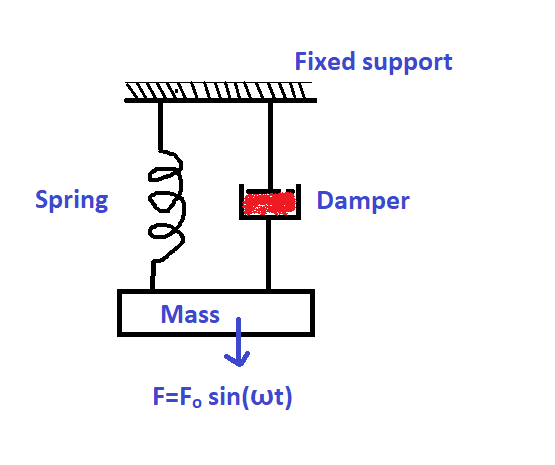
Thus, any machine component can be modelled as a spring-mass-damper system as shown in the following figure.
Mass
It’s obvious that any machinery component will have a certain mass that resists any external load with a magnitude of F = Ma (i.e., Mass times acceleration)
Stiffness
When a load is applied to a component, it undergoes bending or deflection or twisting depending on the type and direction of the applied load and the component resists it in terms of stiffness with a magnitude F = Kx (i.e., stiffness times the displacement of the mass). Spring in the figure-1 represents the stiffness of a component.
Damping
Damping reduces the velocity of a component by dissipating the vibration energy in the solid medium over time thus resisting the motion of the system with a magnitude of F = C 
(i.e., Damping coefficient times the velocity) Piston and oil assembly in the figure-1 represent damping. In general, the engineering components used for the construction of machinery have a damping ratio of less than 1. i.e., underdamped condition. The following table represents the damping ratio of some commonly encountered engineering materials.
| Material | Damping Ratio  |
| Steel Spring | 0.005 |
| Neoprene | 0.05 |
| Natural Rubber | 0.05 |
| Prestressed Concrete | 0.02 to 0.05 |
Response of a system to a Harmonic Load
Consider a harmonic load (load varies as a sin or cosine function with respect to time) of magnitude 
is applied to a system as shown in the following figure.
Where
represents the maximum amplitude of the force
represents the forcing frequency at which force is applied to a system.
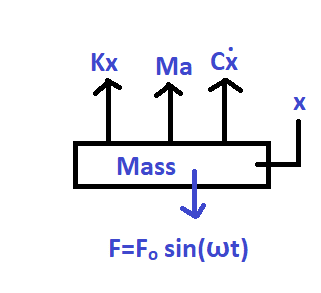
The system resists the applied harmonic load as shown in the following figure. It will undergo to and fro motion about its mean position called vibration.
Note: Here a component can be assumed as a simple spring-mass-damper model system. X represents the displacement of the system in the vertical direction.
Governing Differential Equation of a Spring Mass Damper System Under Harmonic Load
At dynamic equilibrium conditions,
———(Eq-1)
The harmonic load that is applied to the system externally can be treated as an induced force in a machine due to defects like unbalance in the impeller, misalignment in the pump, a bend in the shaft, structural looseness…etc that acts on a machinery component. Most of the induced forces due to defects vary harmonically. If the magnitude of induced force (i.e., RHS of the above equation) is greater than the LHS, then a response of a machinery component is observed in the form of vibration. If the magnitude of RHS is less than LHS, the vibration of a component may not be experienced or sensed.
The mathematical solution of equation-1 represents the system response to the induced or excited harmonic load.
The solution of equation-1 contains two parts. i.e., complementary solution and particular solution. The complementary solution represents the transient state of a system and the particular solution represents the steady-state response of a system.
Complementary solution:
![\, u(t)=e^{-\xi \omega _{n} t}[u(0) cos(\omega _{D}\,t)+\frac{\dot{u}(0)+\xi \omega _{n} u(0))}{\omega _{D}}sin\omega _{D}t]](https://amechieneer.com/wp-content/ql-cache/quicklatex.com-f34b9d6c5e5f953eadd81b27882c577b_l3.png "Rendered by QuickLaTeX.com")
.
Where
represents the initial displacement of the system and
represents the initial velocity of the system which can be found out from the initial conditions of a system.
represents the damped natural frequency of a system.
represents the damping ratio of the system.
Note on Complementary Solution:
- The complementary part of the solution is a function of time, thus it is called the transient response of a system.
- The amplitude of a system decays exponentially with respect to the time so the transient response will not last long in the system.
- The system vibrates at the damped natural frequency but not at the forcing frequency or natural frequency.
Particular solution:
![\, \frac{F_{0}}{k} [\frac{1-(\frac{\omega}{\omega _{n}} )^{2}}{[1-(\frac{\omega}{\omega _{n}} )^{2})^2 +(2\xi (\frac{\omega }{\omega _{n}}))^2]}] sin(\omega t) + \frac{F_{0}}{k} [\frac{-2\xi \frac{\omega }{\omega {n}}}{[1-(\frac{\omega}{\omega {n}} )^{2})^2 +(2\xi (\frac{\omega }{\omega _{n}}))^2]}] cos(\omega t)](https://amechieneer.com/wp-content/ql-cache/quicklatex.com-fd787cb38a01fe9c3d23e84c13bfdd4c_l3.png "Rendered by QuickLaTeX.com")
.
By using trignometric rules above equation can be rewritten as,
![u(t)= \frac{\frac{F_{o}}{k} sin(\omega t-\phi )}{\sqrt{[1-(\frac{\omega}{\omega {n}} )^{2})^2 +(2\xi (\frac{\omega }{\omega {n}}))^2]}}](https://amechieneer.com/wp-content/ql-cache/quicklatex.com-1c1319e6d1eb66f03c68958cbc952d65_l3.png "Rendered by QuickLaTeX.com")
Where 
represents the time lag between the applied harmonic force and the system response
Note on Particular Solution:
- The particular solution is independent of time so it is called the steady-state response. Thus, the system vibrates as long as the system is running.
- The system vibrates at a frequency equal to the forcing frequency
Total solution = Complementary part + Particular part
