Critical Speed Of A Shaft

Critical Speed or Whirling Speed

The critical speed is the angular velocity that excites the natural frequency of the rotating objects like rotors, shafts…etc., resulting in severe vibration of the shaft in the transverse direction. Critical speed is also known as the whirling speed of the shaft. Let us derive the governing equation of the critical speed. Critical speed is nothing but the transverse frequency of a rotating shaft.

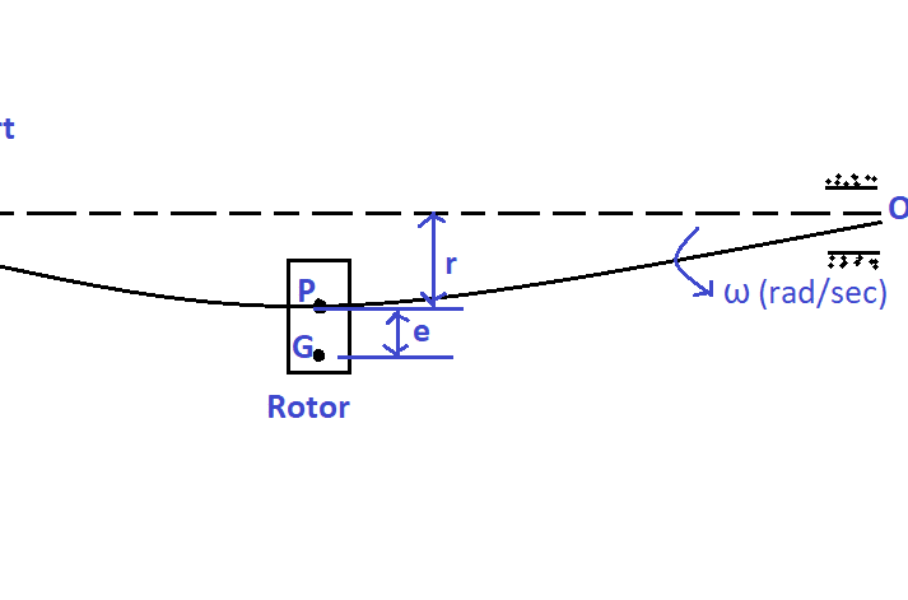
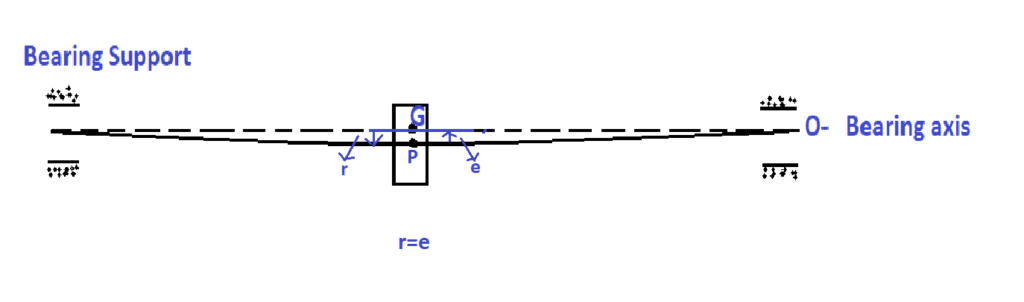
Consider a single rotor & shaft system without damping as shown in the following figure.

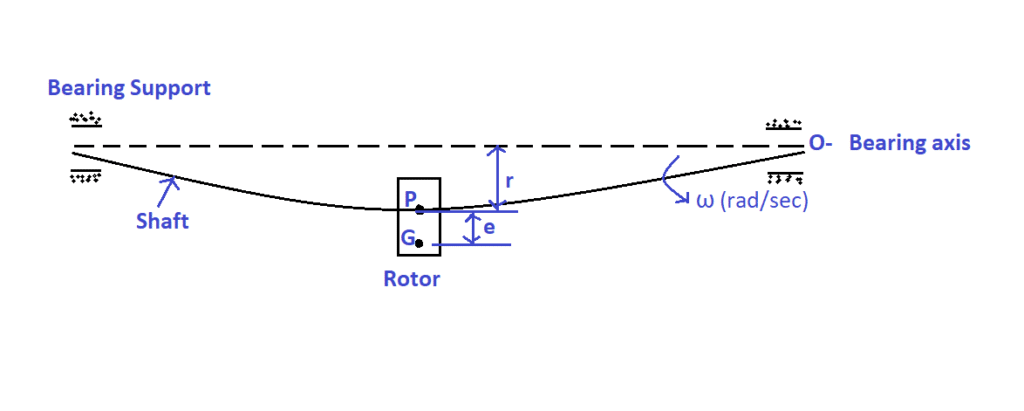
Figure 1 Single Rotor Shaft System — ***Figure 1: Single Rotor Shaft System***

Where,

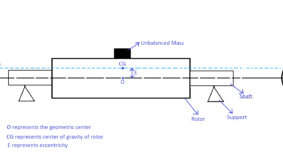
P represents the geometric centre of the rotor

G represents the centre of gravity of the rotor

r represents the distance of the geometric centre from the bearing axis

e represents the eccentricity, i.e., the distance between the geometric centre and the centre of gravity.

Assumptions

The following assumptions are made to derive the governing equation of the critical speed of a single rotor system.

The mass of the shaft is negligible as compared to the mass of the disc. (The natural frequency of the shaft is considered far higher than the disc)
The shaft is considered as a torsional spring.
Static deflection of the shaft is negligible (the shaft is considered stiffer)
Due to the eccentricity of the disc, the centrifugal force comes into the picture.
Centrifugal force tries to pull the disc and the rotor away from the bearing axis until the system reaches dynamic equilibrium.
The magnitude of centrifugal force= 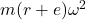$m (r+e) \omega ^{2}$ where m represents the mass of the disc.
The shaft resists the pull of the disc with a magnitude = 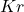$K r$ (From assumption no. 3 shaft resists the deflection due to stiffness property).

Derivation of Critical Speed

At dynamic equilibrium conditions,

The centrifugal force of the rotating disc = Resistance offered by the shaft

$m(r+e)\omega ^2=r. K$

$m\omega ^2r+me\omega ^2=r.K$

$m\omega^2r-rK=-me\omega^2$

$r(m\omega^2-K)=-me\omega^2$

$r=\frac{me \omega^2}{K-m\omega^2}$

$r=\frac{e}{(\frac{\omega_n}{\omega})^2 -1}$ —————Eq-1

Conclusions from the Eq-1

r represents the dynamic deflection of the shaft.
Natural frequency i.e 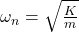$\omega_n =\sqrt {\frac{K}{m}}\,$ where K is the stiffness of the shaft and m represents the mass of the disc. Hence the natural frequency is for the whole system but not for the disc alone.
In general, shafts are designed as short as possible because the deflection of the short shaft is small as compared to the long shaft of the same disc mass since the stiffness is high (Bending stiffness 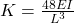$K=\frac{48EI}{L^3}$ . Hence the natural frequency of the system with a short shaft system is high, resulting in less dynamic reflection (r).

Consider the following four cases.

Case-1 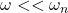$\omega << \omega_n$

In this case, as per equation-1, dynamic deflection (r) is + ive. (i.e., r and e are in the same direction) as shown in the following figure. The heavy side (i.e., the centre of gravity) is away from the bearing axis.

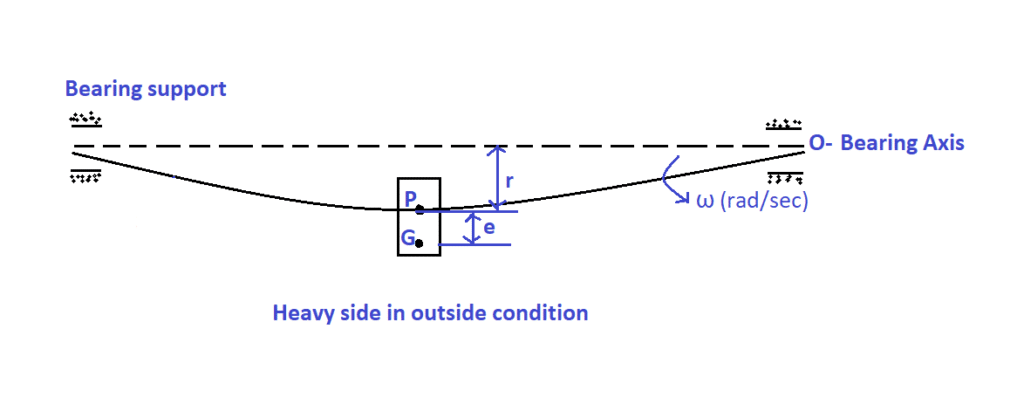
Figure 2 Heavy side in outside condition — ***Figure 2: Heavy side in outside condition***

Since the heavy side is outside, the centrifugal force tries to pull the shaft away from the bearing axis.

Case-2 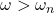$\omega > \omega_n$

In this case, as per equation-1, dynamic deflection (r) is -ive. (i.e., r and e are in opposite directions) as shown in the following figure. The heavy side (i.e., the centre of gravity) is towards the bearing axis.

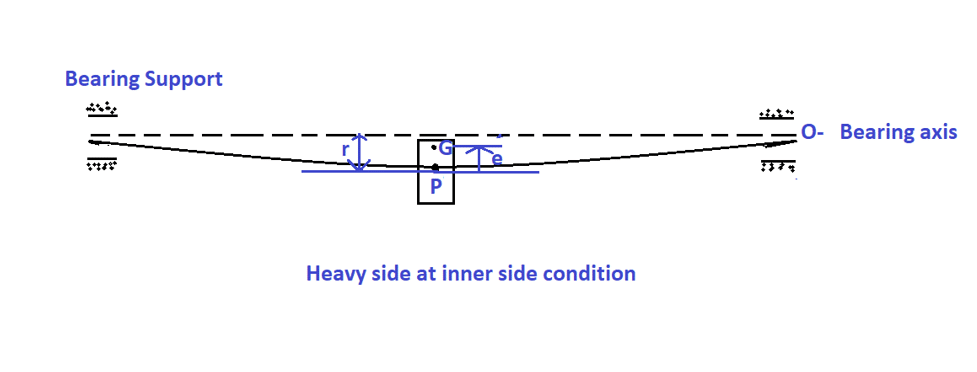
Figure 3 Heavy side at inner side connection — ***Figure 3: Heavy side at inner side connection***

Since the heavy side is inside, the centrifugal force tries to pull the shaft towards the bearing axis. Thus, the dynamic deflection (r) is relatively less as compared to case 1.

Case-3 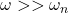$\omega >>\omega_n$

In this case, as per equation-1, dynamic deflection (r) approximately equals eccentricity (e) as shown in the following figure.

Figure 4 r e condition — ***Figure 4: r = e condition***

The centre of gravity coincides with the bearing axis. Thus, the dynamic deflection r is much less than that of the above two cases.

Case-4 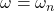$\omega = \omega_n$

In this case, as per equation-1, the value of r is infinite . i.e., resonant or critical speed condition where the shaft vibrates violently.

Note: In general, gas turbines and steam-powered turbines at power plants run at high speeds, i.e., $\omega >>\omega_n$ . To operate at high speeds, the rotor must first pass through the resonant condition, i.e., $\omega = \omega_n$ . To avoid catastrophic failure due to resonant conditions, such high-speed rotors are operated so fast enough to cross the resonant state as soon as possible.

Note: As a result, before commissioning any rotating equipment, whether it be a steam turbine, a ship’s propelling system, or heavy-duty centrifugal pumps, it is vital to determine the critical speed of the shaft.

Why does critical speed exist?

According to equation-1, if the value of e is zero, i.e., eccentricity is theoretically zero, then the shaft deflection (r) is zero, resulting in no transverse vibration of the shaft. It is really achievable if the geometric centre, the rotor’s centre of gravity, and the shaft’s rotating axis all coincide. However, rotor eccentricity can arise for a variety of causes, including those listed below.

Imbalance in rotor
Error in rotor-to-shaft installation
Deposition of foreign material on the rotor, for example, settlement of dust particles on the periphery of an impeller in an off-gas centrifugal fan.

Tips for avoiding shaft failure due to critical speed

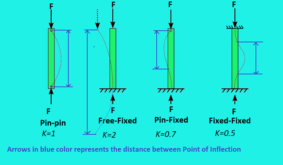
Use a shorter length shaft to improve shaft stiffness, resulting in a critical speed that is distant from the regular working speed.
The stiffness of the shaft depends on the type of shaft like cantilever type ( 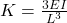$K= \frac{3EI}{L^3}$ ), simply supported type ( 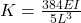$K= \frac{384EI}{5L^3}$ ) & fixed end type and loads on it like point load and uniformly distributed load.
If a critical speed lies between zero and the operating speed, pass through it fast.

Test your understanding of critical speed by taking this Quiz.

FAQ

1. What is critical speed?

Critical speed refers to the specific rotational speed at which a rotating object, like a shaft, propeller, or gear …etc. begin to vibrate excessively. This happens when the rotation speed aligns with the object’s natural frequency, essentially causing resonance.

2. Critical speed of the shaft formula?

$r=\frac{e}{(\frac{\omega_n}{\omega})^2 -1}$

Where
r represents the distance of the geometric centre from the bearing axis
e represents the eccentricity, i.e., the distance between the geometric centre and the centre of gravity.
$\omega_n \,$ represents the natural frequency of a rotating object.
$\omega \,$ represents the operating speed of the rotating object.

Sign Up

Sign In

Forgot Password

The Mechanical Engineer Latest Articles

Table of Contents

Critical Speed or Whirling Speed

Assumptions

Derivation of Critical Speed

Conclusions from the Eq-1

Case-1

Case-2

Case-3

Case-4