Columns are the silent workhorses of the structural world, supporting massive loads and keeping buildings and bridges standing tall. But what happens when a column experiences too much load? The answer lies in a phenomenon called buckling.

What is Column Buckling?

The buckling of columns is a phenomenon in structural engineering where a slender column (a long, thin structural element) experiences a sudden lateral deflection (bending) under compressive load. This means instead of simply compressing under the load, the column bends sideways and loses its ability to hold the load effectively.

Why Does Buckling Happen?

There are two main reasons why the buckling of columns occurs:

Column Buckling due to Imperfections

No column is perfectly straight. Even microscopic imperfections can act as starting points for bending when a column is subjected to high compressive loads.

Column Buckling due to Material Limitations

Real materials have a finite strength. Under high enough loads, even a perfectly straight column can buckle due to the limitations of the material itself.

Euler’s Critical Buckling Load Formula

Euler’s buckling load formula, derived by Leonhard Euler in 1744, calculates the maximum axial compressive load a slender column can support without buckling under ideal conditions. Here’s a breakdown of the formula and its components:

Formula:

$P_{cr}=\frac { \pi ^{2} EI _{min}}{(KL)^{2}}$

where:

$P_{cr}$ : Critical buckling load (the maximum load the column can support)

$\pi$ : Mathematical constant (approximately 3.14)

E: Young’s modulus of the column material (a measure of stiffness)

$I_{min}$ : Least area moment of inertia of the column’s cross-section (a measure of its resistance to bending)

K: Effective length factor (accounts for different end conditions)

L: Length of the column between two supports

Factors Affecting Column Buckling

$\pi ^{2}$ : This constant term appears because the buckling mode of the column involves a sinusoidal deflection, and $\pi _{2}$ is a geometric factor related to this shape.

E: The Young’s modulus represents the material’s stiffness. A higher stiffness (higher E) leads to a higher critical buckling load, making the column more resistant to bending and buckling.

I: The area moment of inertia reflects the distribution of material within the cross-section. A larger moment of inertia (larger I) signifies a more spread-out material distribution, increasing the column’s resistance to bending and, consequently, raising the critical buckling load.

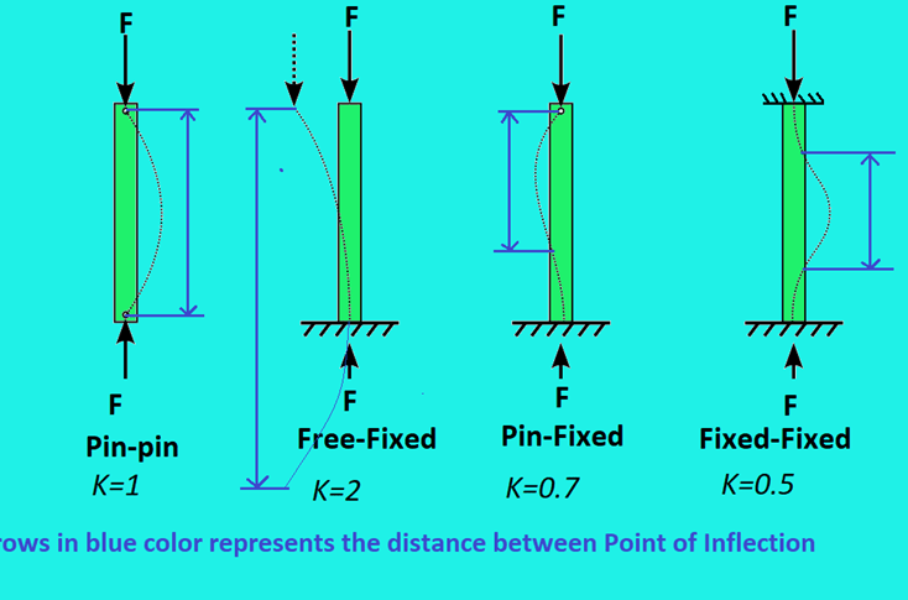
K: The effective length factor (K) accounts for various end conditions. Higher K values (corresponding to less constrained end conditions) represent a higher effective length, leading to a lower critical buckling load. Refer following figure.

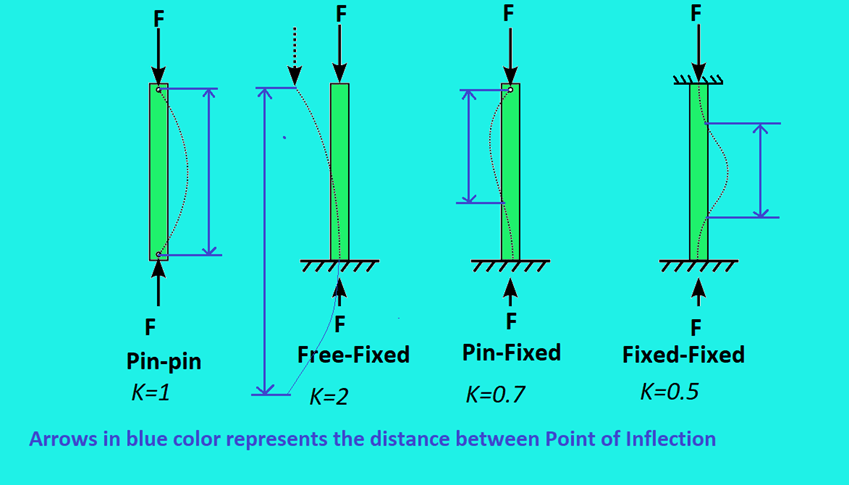
***Figure 2: Buckling of Columns under Different End Conditions***

L: The actual length of the column directly affects its buckling behaviour. Longer columns (larger L) have a lower critical buckling load due to increased flexibility.

EI: Product of Modulus of elasticity and the area moment of inertia represents the flexure rigidity. It represents the bending stiffness.

Assumptions and Limitations of Euler Buckling Load:

It’s important to understand that Euler’s formula makes several assumptions:

The column is perfectly straight and free from initial imperfections.
The material is homogeneous and isotropic (same properties throughout and in all directions).
The load is applied axially at the centre of the column.
The material behaves elastically (no permanent deformation). The material remains within its elastic range, meaning it returns to its original shape after the load is removed.

Euler’s Buckling Stress Formula

$\frac {P_{cr}}{A}=\frac { \pi ^{2} EI}{(KL)^{2}A}$

$\sigma_{cr} = \pi ^{2} E \frac {I}{A(LK)^2}$

$\sigma_{cr} = \frac {\pi ^{2} E} {s^2}$

Where s represents the slenderness ratio of column $s=\frac{KL}{r_{g}}$

$r_{g} \,$ represents least radius of gyration of the cross section

Euler buckling stress is independent of the material’s strength

The Euler buckling formula predicts the critical buckling load based on the elastic deformation of the column. In this idealized scenario, the material remains within its elastic range, meaning it returns to its original shape after the load is removed.

Material strength, typically characterized by yield strength or ultimate tensile strength, comes into play when the material undergoes plastic deformation. This occurs beyond the elastic limit, where the material permanently deforms under stress.

Yielding Vs Buckling of Columns

Columns under axial compressive load can fail due to either by crushing (exceeding the ultimate strength of material) or by buckling (lateral deflection or bending).

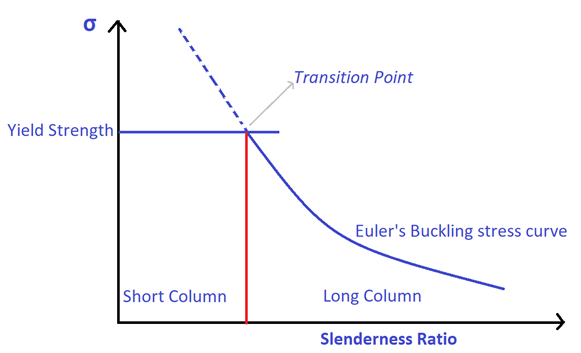
***Figure 3: Buckling Stress vs Slenderness Ratio***

The region below the solid blue line is a safe zone where the given column withstands the axial compressive load without undergoing buckling or crushing.

Following are the conclusions derived from the above graph.

The lower slenderness ratio columns are called short columns. Short columns or stockier columns fail first by crushing instead of crushing. Because from the above graph, short columns fail first by crushing.
The higher slenderness ratio columns are called long columns. Long columns or slender columns fail first by buckling. Because their buckling strength is lower than the yield strength of the column.

Transition Point of Short Column and Longer Column

The red coloured line in the above graph represents the transition between the short and long columns. At the transition point, the yield strength and buckling strength of a column is equal. The transition slenderness ratio can be found by following the relation.

$\sigma _{y} = \frac {\pi ^{2} E} {s^2}$

$s^2 = \frac{\pi ^2 E}{\sigma _{y}}$

$s= \sqrt{ \frac{\pi ^2 E }{\sigma _{y}}}$

Difference between Buckling and Bending

While both buckling and bending involve the deformation of a material, they differ in their key characteristics and the way they occur:

Bending

Type of deformation: Bending is a continuous deformation where a material curves under the application of a force perpendicular to its longitudinal axis. This force creates a bending moment, causing the material to elongate on one side (tension) and compress on the other (compression). Bending is predictable.

Buckling

Type of deformation: Buckling is a sudden, lateral (sideways) bending of a slender element subjected to a compressive axial load (force pushing along its length) exceeding a critical value. This critical load is determined by the material properties, geometry, and end conditions of the element. Unlike bending, buckling leads to a sudden loss of stability and often fails the element. Buckling is typically irreversible. Once a column buckles, it loses its ability to support the load and can collapse rapidly.

Feature	Bending	Buckling
Type of deformation	Continuous curvature	Sudden lateral bending
Force direction	Perpendicular to the axis	Compressive, along the axis
Material behaviour	Elastic or plastic (depending on the material)	Usually leads to failure (inelastic)
Examples	Beam, diving board, paperclip	Column, straw, chair legs

Table 1: Difference between Bending and Buckling

How to prevent buckling in columns?

Increasing Stiffness

Using thicker or wider cross-sections: Increasing the column’s cross-sectional area (like using a thicker pipe for a column) increases its moment of inertia, which directly correlates to its resistance to bending and buckling.

Choosing stiffer materials: Materials with a higher Young’s modulus (stiffness) are more resistant to deformation under load, making them less susceptible to buckling. Steel and concrete are common choices for columns due to their high stiffness.

Reducing Effective Length: Providing intermediate supports. Dividing a long column into shorter segments with supports in between effectively reduces the unsupported length. This significantly increases the critical buckling load and prevents premature buckling.

Fixing the ends of the column: Columns with fixed ends (both ends securely fastened) have a lower effective length than those with pinned or hinged ends, leading to a higher critical buckling load.

Using Bracing

Diagonal bracing: These are inclined members connecting the column to other structural elements, forming a triangular shape. This arrangement effectively resists lateral forces trying to bend the column. These bracing elements act like rigid supports, preventing the column from swaying sideways. By restraining this lateral movement, the bracing effectively increases the stiffness of the entire system.

Perimeter bracing: This involves enclosing the column with a framework of beams and columns, creating a rigid cage that restricts lateral movement.

Cross-bracing: This involves connecting multiple columns together with horizontal and diagonal members, forming a grid-like structure that provides overall stability and prevents individual columns from buckling.

Benefits of bracing

Increased critical load: Bracing significantly increases the critical buckling load of a column. This is the maximum load the column can withstand before buckling occurs. By restricting lateral movement, bracing prevents the initial deflection that triggers buckling, allowing the column to support larger loads before failure. By adding the bracing member to the middle of the pin-pin end connected column, the length becomes L/2 resulting in an increase of critical load to a factor of 4 as shown in the following figure since the buckling load is inversely proportional to length squared.

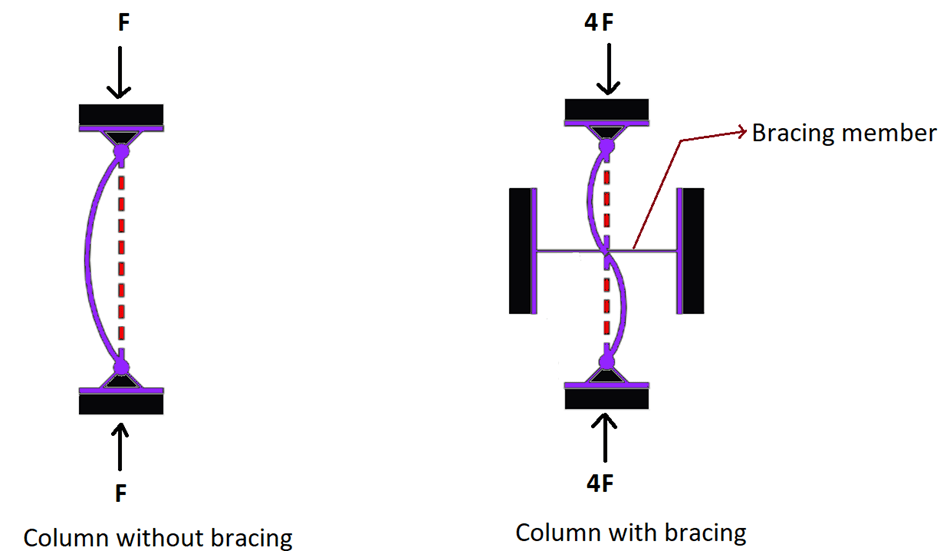
***Figure 4: Columns with and without Bracing Members***

Improved stability: Bracing enhances the overall stability of the structure by preventing individual columns from buckling. This ensures the structure can maintain its shape and function even under significant loads.

Types of Column Buckling

There are three types of column buckling. They are

Flexural Buckling
Torsional Buckling
Flexural-Torsional Buckling

Flexural Buckling

Flexural buckling is the most prevalent type, where a long, slender column bends sideways in a single plane. The discussions and Euler’s buckling formula we explored earlier apply specifically to this type of buckling.

Torsional Buckling

This type of buckling involves twisting of the entire column cross-section about its longitudinal axis. It’s more prevalent in thin-walled columns or those with non-circular cross-sections (like tubes). The column twists along its longitudinal axis instead of bending laterally. This can be catastrophic as the entire column loses its ability to resist the load. Torsional buckling often occurs when the compressive load isn’t perfectly centred (eccentric load) or when the column is subjected to additional twisting moments.

Flexural-Torsional Buckling

This buckling mode combines both bending and twisting deformations. It often occurs in columns with non-uniform stiffness in different directions, such as channels, tees, or single-angle shapes. The eccentric load or imperfections can initiate both bending and twisting simultaneously or sequentially. As the column bends, its torsional resistance might be reduced, leading to further twisting and a more complex buckling behaviour. Refer

FAQ

1. Why higher slenderness ratio columns are more susceptible to buckling?

Reduced bending moment: A lower slenderness ratio implies a shorter length or a larger radius of gyration. (The least radius of gyration is a geometric property that reflects the distribution of the column’s cross-sectional area away from its centroidal axis. It essentially indicates how effectively the material is distributed to resist bending.) Both of these factors contribute to a higher stiffness of the column. This increased stiffness makes it more difficult for the column to bend under the same compressive load, thereby reducing the bending moment experienced.

Test Your Knowledge in Column Buckling

Sign Up

Sign In

Forgot Password

The Mechanical Engineer Latest Articles

Table of Contents